| [1] | Received April, 1959. Part of the material contained herein was presented at the meeting of the Association, September 1-3, 1959. |
A Fortran-Compiled List-Processing Language [1]
| Authors: | H. Gelernter, J. R. Hansen, C. L. Gerberich |
|---|
International Business Machines Corp., Yorktown Heights, N.Y.
Abstract. A compiled computer language for the manipulation of symbolic expressions organized in storage as Newell-Shaw-Simon lists has been developed as a tool to make more convenient the task of programming the simulation of a geometry theorem-proving machine on the IBM 704 high-speed electronic digital computer. Statements in the language are written in usual FORTRAN notation, but with a large set of special list-processing functions appended to the standard FORTRAN library. The algebraic structure of certain statements in this language corresponds closely to the structure of an NSS list, making possible the generation and manipulation of complex list expressions with a single statement. The many programming advantages accruing from the use of FORTRAN, and in particular, the ease with which massive and complex programs may be revised, combined with the flexibility offered by an NSS list organization of storage make the language particularly useful where, as in the case of our theorem-proving program, intermediate data of unpredicable form, complexity, and length may be generated.
I. Introduction
Until recently, digital computer design has been strongly oriented toward increased speed and facility in the arithmetic manipulation of numbers, for it is in this mode of operation that most calculations are performed. With greater appreciation of the ultimate capacity of such machines, however, and with increased understanding of the techniques of information processing, many computer programs are being now written that deal largely with entities that are purely symbolic and processes that are logistic rather than arithmetic. One such effort is the simulation of a geometry theorem-proving machine being investigated by the authors and D. Loveland at the Yorktown IBM Research Center [1, 2]. This massive simulation program has a characteristic feature in common with many other such symbol-manipulating routines, and in particular, with those intended to carry out some abstract problem-solving process by the use of heuristic methods [3, 4]. The intermediate data generated by such programs are generally unpredictable in their form, complexity, and length. Arbitrary lists of information may or may not contain as data an arbitrary number of items or sublists. To allocate beforehand to each possible list a block of storage sufficient to contain some reasonable maximum amount of information would quickly exhaust all available fast-access storage as well as prescribe rigidly the organization of information in the lists. A program failure caused by some list exceeding its allotted space while most of the remainder of storage is almost empty could expected as not uncommon occurence.
Faced with this program, Newell, Shaw, and Simon, in programming a heuristic theorem-proving system for the propositional calculus, simulated (by programming) a kind of associative memory (henceforth referred to as an NSS memory) in which lists of arbitrary length and organization could be generated by annexing registers from a common store [5]. The price paid for tihs very substantial increase in programming flexibility is an apparent decrease (by a factor of about one-half) in usable high-speed storage and a real decrease in the speed of indexing consecutive items in a given list. The debilities are due to the fact that consecutive items of data are not in consecutive memory registers, as in a standard memory, but are, rather, connected by a string of location words. These location words, however, determine the organization of the data, and in programs such as the one for which the NSS memory was developed, the organization of the data contains a good deal of the information about it. In addition, the location words themselves can carry several bits of useful data and can be used to annex a given item on several different lists, making repetition of the data unnecessary. Consequently, as the number and complexity of the generated lists increases, the density of useful information stored in a NSS memory approaches one word per register.
The decrease in processing speed is not so easily shrugged off. By modifying the logical design of the instruction roster to permit, for example, indirect addressing from both the left and the right half of a register (decrement and address, respectively, in the IBM 704), much improvement may be realized in this respect. But the ability to quickly withdraw a specified item of data by computing its address is inexorably lost. Lacking the built-in refinements of indirect addressing and other special instructions designed to manipulate NSS lists, Newell, et al, designed an interpretive routine for their computer (the Rand Johnniac) to lighten the task of translating their programming wishes into the arithmetic-oriented instruction code of the Johnniac. In fact, a series of these interpretive languages were written and were called by their authors "Information Processing Languages" [5]. Unfortunately, the introduction of an intermediate interpreter for each command further extracts its toll in computing speed, so that relatively simple operations require an inordinate amount of time. This is in large degree responsible for the great disparity in time required by the propositional calculus theorem prover of Newell et al, and that of Wang [6] to prove the same theorems, Wang's machine being from three to five orders of magnitude faster. The designers of the Information Processing Languages (IPL) estimate that a complex operation like choosing a strong move in a game of chess would require of the order of an hour when programmed in their interpretive system.
When the present authors embarked upon their effort to simulate a geometry theorem-proving machine, it was early decided that an NSS organization of memory would best serve their purpose, and consideration was given to the translation of a Johnniac IPL for use with the IBM 704 computer. However, J. McCarthy, who was then consulting for the project, sugested that FORTRAN could be adapted to serve the same purpose. He pointed out that the nesting of functions that is allowed within the FORTRAN format makes possible the construction of elaborate information-processing subroutines with a single statement. The authors have since discovered a further substantial advantage of an algebraic list-processing language such as one written within the frameowrk of FORTRAN. It is the close analogy that exists between the structure of an NSS list and a certain class of algebraic expressions that may be written within the language. We shall return to this point in greater detail below. Not to be overlooked is the considerable sophistication incorporatred in to the FORTRAN compiler itself, all of which carries over, of course, into our FORTRAN-compiled list-processing language. It is reasonable to estimate that a routine written in our language would run about five times as fast as the same program written in an interpretive language.
II. The Newell-Shaw-Simon Associative Memory
Although the NSS scheme for a programmed associative memory has been described in the literature, certain modifications that we have introduced make it necessary for us to repeat the description in some detail. We shall, in this section, follow the paper of Newell and Shaw to which we have already referred. It is well to point out, however, that the authors feel that most of the properties that Newell, et al, ascribe to their Information Processing Language are rather properties of the NSS associative memory itself. They are reasonably independent of the particular scheme devised for the manipulation of information within the structure of the memory. For a certain limited number of cases, we have, in fact, found it more convenient to write subroutines in the basic symbolic machine code. The advent of FORTRAN III makes it possible to do this within the framework of our list-processing language.
The storage registers comprising an NSS memory all fall into one of two basic categories, those containing the gross data for the information process (called data words), and those that serve to associate strings of data into list structures (called location words). A list is the fundamental assemblage of information in storage. Each register of an NSS memory is an element of at least one list; if it is not on some information list, then it is on the list of available storage (LAVST), which serves as a source of raw material for list formation processes and as a sink for dissociated registers when information is destroyed.
Data words (or d-words) are 36-bit units of information. The interpretation of this information is determined by the list containing it, its location on a particular list, or by an identifying tag in the location word associated with the datum. They may be treated as signed floating point numbers, or as any arbitrarily fixed set of information fields packed into the register.
Location words (or l-words) supply the links between units of information in a list. For the purpose of our FORTRAN-compiled list-processing language (FLPL), the format of a location word is fixed by a set of conventions (fig. 1). In the following discussion, the field of an l-word containing the address of a register will be said to point to that register.
A list is characterized by a directed linear string of l-words such that the decrement field of each l-word on the list points to the next l-word on that list. The terminating l-word contains a zero in the decrement field. The name of the list is the address of its initial l-word.
| S | 1-2 | 3-17 | 18-20 | 21-35 |
| 1 bit of data | Type code | Address of location word for next entry on this list. Set to zero in terminating l-word. | 3 bits of data | Address of data (or list) entered on this list, or else 15 bits of data. |
| Sign | Prefix | Decrement | Tag | Address |
Fig. 1. Standard l-word format.
In general, the address field of the i th l-word on the list points to the i th data entry on the list. The entry may be a d-word, or an l-word (if the entry is another list). If a fifteen-bit field will suffice to contain all the information, the address may be used to carry the data itself rather than a reference to the data. The exact nature of the entry is indicated by the type code.
In their published report, Newell and Shaw point out a particular difficulty in using their associative memory [5, p. 240]. Since a given entry may appear on several different lists, it is important, when erasing a list, to distinguish between these data and the entries that appear only once, for if the datum that appears elsewhere is itself erased the remaining lists that contained it would be left pointing into limbo. Our solution to the problem has been to assign a list priority to each data entry by means of a two-bit l-word type code. The first bit of the code determines priority. It is set to 1 if the entry is an integral part of the list containing the location word, and 0 if the entry is "borrowed" from some other list. Every entry will belong to one and only one list, appearing as borrowed data on every other list. No initial data entry is erased until all of its derivative entries have been erased. The second bit of the type code determines the nature of the entry. It is set to 1 if the netry is a list (i.e., an l-word) and 0 if it is a d-word. The type code contains all of the necessary information to control automatic erasing and printout of lists. The 00 type code is used also to indicate direct entry of data into the address of the l-word, since erasure and printout for this case are treated exactly as in the normal 00 "borrowed d-word" case (table 1). Since a list entry pointer generalaly indicatres the first l-word of a specific list, that 15-bit quantity is also the machine name for that list. It is often useful to view a list pointer as data entry in the l-word address field, the datum being, of course, the name of a list.
The remaining sign and tag fields of the l-word are used for information storage. The sign, an especially accessible bit of data, is often used as a "punctuation mark" for the list.
It is instructive, at this point, to examine a typical use of the NSS memory. Our example is chosen from the geometry theorem-proving project mentioned above and illustrates clearly the value of an associative memory for such programs. Displayed below (fig. 2) are two of the lists describing a diagram such as one might construct to aid in finding a solution to a particular problem in elementary Euclidian plane geometry. The lists contain l-words illlustrating each of the possible type-codes, including both modes of the 0-code. We shall describe their structure in some detail, since our example will again prove to be useful at a later point in our discussion of FLPL.
| Type Code | Address Field |
| 11 (3) | Iniital list entry pointer |
| 10 (2) | Initial d-word entry pointer |
| 01 (1) | "Borrowed" list entry pointer |
| 00 (0) | "Borrowed" d-word entry pointer or dat field |
TABLE 1
LPTS is a list containing a coordinate representation of each point in the diagram together with the symbolic name of each point. There are three entries on LPTS, each entry being in itself a list. The machine name of LPTS is the address, α, of the first word of the list. FLPL keeps its own internal "dictionary" to translate mnemonic designations such as LPTS into the machine name. The type-code of each l-word of LPTS is 3, since each individual point list appears initially on LPTS and is considered as belonging to that list. As indicated above, it is convenient to think of LPTS as comprising the three linked l-words α, β, γ, containing as data entries the names α1, β1, and γ1, of the individual point lists, which are in fact the machine names of points A, B, and C, respectively.
A given individual point list, α1 for example, contains the three compoentns of the position vector of that point in a homogeneous coordinate system followed by the symbolic name of the point entered as data in the l-word address field (type-code 0). The vector compopnents are in general entered as initial d-words (type-code 2), but since the third component of a point is always unity in a homogeneous coordinate system the constant 1.0 is entered only once, appearing subsequently as borrowed data (type-code 0).
Every segment in the diagram is listed on LSEG. Each individual segment list, μ1 for example (the segment AB), designates the endpoints of the segment, by "borrowing" the points from LPTS (type-code 1 in l-words μ1 and μ2). Note that the program has not only the machine names of the points (α1 and β1) at its disposal, but the complete set of information conerning these poitns as well, lsince the names are in fact the location of the individual point lists. The sign of the second l-word in each segment list is by convention set negative to indicate the termination of the body of the list, and that the continuation of the list is all descriptive material. SHould available storage become scarse at some stage in the computation, it is again a convention (applying only to diagram lists0 that all description continuations are erased, since they may be recomputed if necessary.
The first entry on a segment description list is the length of the segment. It is identified by its position at hte head of the description list (μ3). Subsequent entries serve to express (in arbitray order) relationships between the given segment and other elements of teh diagram and are identified by the tag. Tags 1 and 4 are interpreted as equality and perpendicularly, repsectively and l-words μ4 and μ5 indicate that the segment AC (machine name, ν1) is both equal and perpendicular to segment AB (μ1). Tag 6 is interpreted as membership in a triangle, and so μ6 will contain in the address field the machine name of triangle ABC, which will appear as a list entry on LTRNGL, a list of all triangles in the diagram. In each case the related element is appended to the description as a "borrowed" list.
The associative properties of an NSS memory are clearly evident in the structure of LSEG. The list entry SEGMENT AB contains, for example, the lists SEGMENT AC, and TRIANGLE ABC as part of the description of segment AB. Each of these lists contain, in turn, the names of other related lists as descriptive information, and so on, so that all levels of associated information that are pertinent to a given element are available, given the name of that element.
In its initial state, the NSS memory comprises one long list of type 0 l-words, the list of available storage (LAVST). The address field of eaech register contains as data the number of register following it on the list, so that the amount of unused storage is always known. In loading the NSS memory (creating new lists), cells are removeed from the head of LAVST. When lists are erased, cells are returned to the head of LAVST. If at any stage of a calculation LAVST is exhausted, new space may be created by erasing some of the less important listls in storage (recomputable descriptions for example). It should be clear that the NSS system offers complete flexibility in the organization of information and complete freedom to re-organize it at any stage. In programming for the geometry theorem-proving machine, the latter advantage has been pressed with great frequency.
III. The FORTRAN List-Processing Functions
Thoughout the remainder of this paper, it will be assumed that the reader is faimiliar with the FORTRAN compiling system for the IBM 704 Data Processing Machine and has at his disposal the reference manuals describing the original system and its extensions, FORTRAN II and III. It must be emphasized that FORTRAN is in itself an information processing language of great versatility and sophistication. Our list-processing functions merely serve to increase the "vocabulary" of the language so that list manipulation processes may be described within the FORTRAN framework as are ordinary computer processes. We are thus able to enjoy the same ease of programming, ease of modification, and extensive debugging aids available to the programmers of standard numerical problems. Since this paper is not intended to serve as a programmer's manual for FLPL, many details essential for its use will be omitted. The description of the language is completed in an IBM internal memorandum, soon to be available.
The dominant characteristic of most of our special list-processing functions is that they are not functions at all in the normally understood sense of the term. For many of them, the value of the function [2] depends not only upon its arguments, but also upon the particular internal state configuration of the computer as they are "evaluated". Indeed, one often uses them solely to effect such a change, discarding the unwanted value of the function. Most of our list-processing functions are, in fact, arbitrary subroutines that can be compounded and manipulated according to the algebraic rules for the compounding and manipulation of functions in the FORTRAN language.
| [2] | In normal use the execution of a compiled FORTRAN function statement produces a number in the accumulator which is the "value" of the function. |
The primitive (coded directly in machine language, and available on the library tape) FLPL functions fall into seven rather well defined groups for performing the operations enumerated below:
- information retrieval
- information storage
- information processing
- information search
- list generation
- service routines
- special purpose functions
By combining the primitive operations according tot he rules of FORTRAN, list-processing operations and subroutines of arbitarry complexity may be constructed. The compoundoperations can be named, if desired, so that they may be used as elements of larger routines.
Given the name of a list, the information retrieval functions enable one to extract the contents of any desired field of information in the list. The following are examples of this class [3]:
XCDRF(J), XCARF(J), XCPRF(J), XCSPF(J), XCTRF(J)
Extract contents of the (decrement, address, prefix, signed prefix, tag) register of the word stored in location J.XCWWF(J), CWWF(J)
Extract entire word at location J. CWWF(J) is used if information is to be treated as floating point number.XTRACTF(J, MASK, ± MOVE)
MASK is a pattern of 18 or fewer contiguous bits in a 36-bit field; MOVE is an integer ≤ 18. Extracts the information field indicated by MASK from the word at location J and converts it into standard FORTRAN fixed-point format (entirely in left half-register), by shifting MOVE positions to the right or left, where positive MOVE is to the right. Thus, if MASKT is the bit pattern 00 00 00 70 00 00, then XTRACTF(K, MASKT, -3) is completely equivalent to XCTRF(J).Refering to figure 2, these functions perform the following operations [4]:
- XCARF(LPTS) ⇒ α1, the name of the first point on LPTS (note that the compiler susbtitutes the machine name α for LPTS).
- XCARF(XCDRF(LPTS)) ⇒ β1, the name of the second point on LPTS.
- XCARF(XCDRF(XCDRF(XCDRF(XCARF(LPTS))))) ⇒ A, the symbolic name of the first point on LPTS.
- CWWF(XCARF(XCDRF(XCARF(LPTS)))) ⇒ floating point y-component of first point on LTPS.
| [3] | The complete set of functions of each class is described in the previously mentioned internal report. |
| [4] | The symbol ⇒ should be read "has the value". |
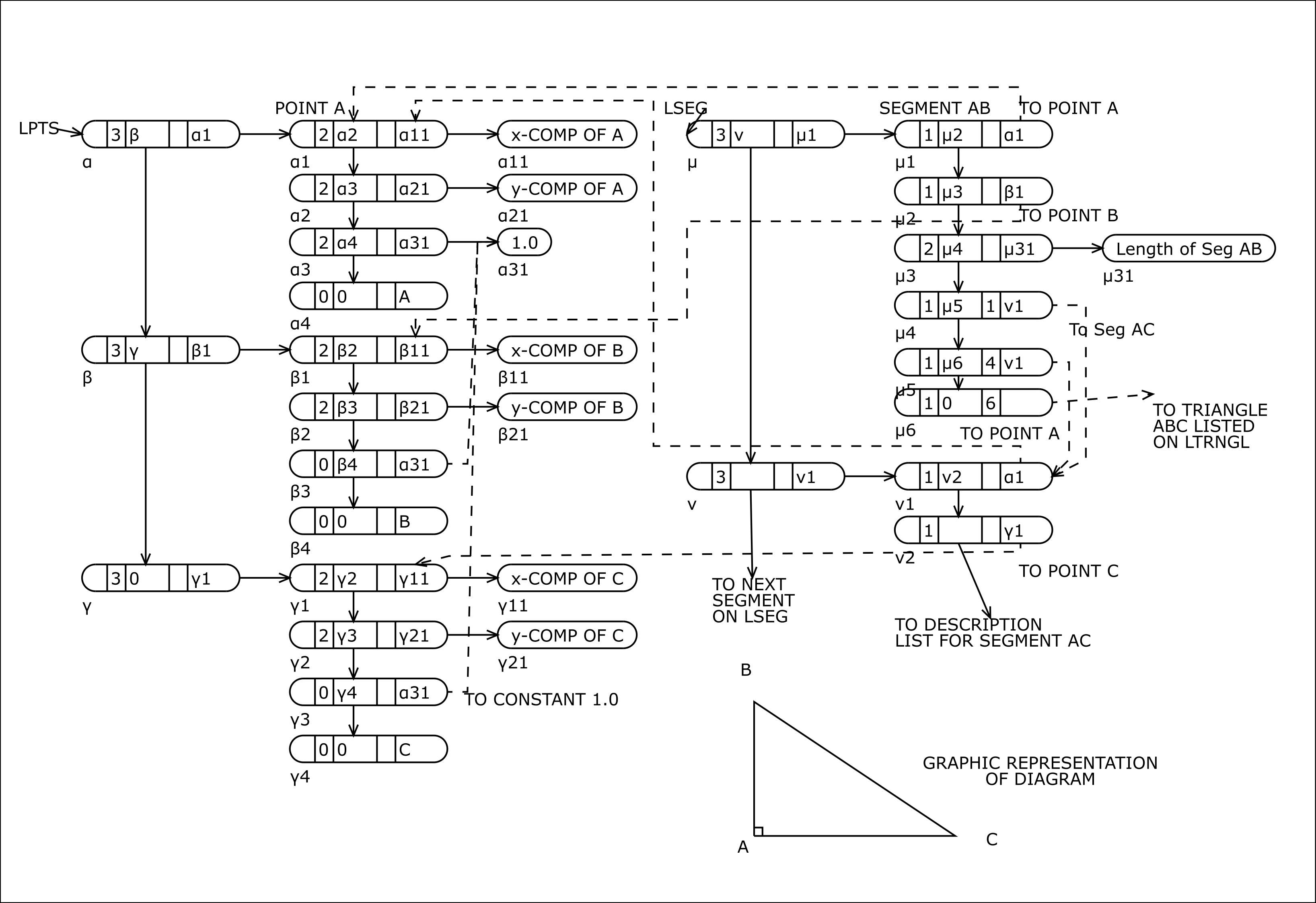
Fig. 2. In each l-word, the information fields contain sign, prefix (type code), decrement (next l-word on list), tag, and address (entry pointer or data), in the order stated. Address of each memory cell is designated at lower left.
Also in the category of information retrieval are the following generalized forms of XCARF and XCDRF:
XCARnF(J), XCDRnF(J)
where n is an integer ≤ 9. Equivalent to n iterations of the base function; thus XCAR3F(J) is equivalent to XCARF(XCARF(XCARF(J))).XCADF(J), XCADAF(J), XCADADF(J), XCDAF(J), XCDADF(J), XCDADAF(J)
Equivalent to a sequence of alternations of XCARF and XCDRF, specified by the sequence of "D's" and "A's" in the name of the function; thus XCDADF(J) is equivalent to XCDRF(XCARF(XCDRF(J))).
With the generalized functions available, examples 2, 3, and 4 above could be written XCADF(LPTS), XCARF(XCDR3F(XCARF(LPTS))), and CWWF(XCADAF(LPTS)), respectively.
If the same operation is to be performed on every entry on a list, an indexing pointer is set up and the operation is performed with the index as a dummy variable. Thus, the following program could be used to find a point on LPTS with x-component greater than two units.
INDEX = LPTS. Initialize index pointer.
10 IF(CWWF(XCAR2F(INDEX)) - 2.0) 15, 15, 20. Go to statement 20
if x-component is greater than 2.0; otherwise go to 15.
15 INDEX = XCDRF(INDEX). Move index to next ``l``-word on ``LPTS``.
20 NAMEPT = XCARF(INDEX). Retrieve machine name of point.
GO TO (EXIT TO ROUTINE FOR PROCESSING NAMEPT).
25 (EXIT WHEN LPTS CONTAINS NO POINT WITH X-COMP > 2.0).
If the coordinates of a point are to be processed frequently, one might define specific component-extraction functions within FORTRAN to ease the task, thus, COMPXF(J) = CWWF(XCAR2F(J)) and COMPYF(J) = CWWF(XCADAF(J)) will extract the x- and y-component of a point-vector, respectively. Statement 10 above could then be written:
10 IF(COMPXF(INDEX)-2.0) 15, 15, 20.
The information storage primitives are used to store or modify information in already existing list structures. The value of each function is the previous content of the information field in which the new information is to be stored [5]. They include the following:
XSTORDF(J,K), XSTORAF(J,K).
The 15-bit quantity K is stored in the (decrement, address) of the word at location J. Its value is the previous content of the (decrement, address) field of J.XSTORTF(J,I), XSTOSPF(J,I).
The 3-bit quantity I is stored in the (tag, sign and prefix) field of the word at location J. Its value is the previous content of the (tag, sign and prefix) register.XSWWF(J,L), SWWF(J,D).
The full word of fixed point data L, (or the full word of floating point data D) is stored in location J. The value of the function is the previous content of J.
| [5] | Information storage in FLPL is, therefore, nondestructive. |
The following FLPL statement will interchange the y-components of points A and B in LPTS:
JUNK = XSTORAF(XCDADRF(LPTS), XSTORAF(XCDAF(LPTS), XCADADF(LPTS)))
------------ ----------- -------------
β2 α2 β21
-----------------------------------
α21
The value of the entire function is β21, the address of the y-component of B. Since we do not wish to further process this number, it is discarded into a "bottomless pit" by setting the function equal to a standard variable, "JUNK".
Also classified as information storage functions are:
XORTAGF(J,I), XORSPXF(J,I).
The 3-bit quantity I is "ORed" into the (tag, sign and prefix) of the word at location J. Its value is the new (tag, sign and prefix) at location J.
Logical processing of data within the framework of FLPL is effected by the information processing functions, which include the following:
XORF(J,K), XANDF(J,K).
The logical (OR, AND) operation is performed on the 36-bit quantities J and K. The sign bit of the value is the result of the (OR, AND) operation on the sign bits of J and K.XMASKF(J, MASK, ± MOVE).
MASK is a pattern of 18 or fewer contiguous bits in a 36-bit field; MOVE is an integer ≤ 18. Extracts the information field indicated by MASK from the quantity J (not from the word at location J) and converts it into FORTRAN fixed point format by shifting MOVE positions (positive move is to the right).
XMASKDF(J), XMASKAF(J), XMASKTF(J), and XMASSPF(J) are special cases of XMASKF for converting the decrement, address, tag, or signed prefix of the quantity J into FORTRAN fixed-point format.
In addition to the above, FLPL has, of course, at its disposal the standard FORTRAN arithmetic information processing operations for both fixed and floating-point data.
Although the information search functions may easily be defined within FLPL, it is convenient to include a number of the more frequently used search processes among the primitives. The most useful are:
XLASLCF(J)
Searches down the list of l-words headed by (and named) J. Its value is the address of the last l-word on J (determined by its zero decrement).XTGSCHF(J,I), XSPSCHF(J,I).
I is a 3-bit quantity ≤ 7. Searches list J for the first l-word with (tag, signed prefix) equal to I. Its value is the address of the l-word with the required (tag, signed prefix), unless none can be found, whence it is set to zero.XBTSCHF(J,M), XBSPSHF(J,M).
M is the octal representation of a one-bit mask on a 3-bit field (equals 1, 2, or 4). Searches the list J for the first l-word with a abit in position M of its (tag, signed prefix). Its value is the address of the l-word with the required (tag, signed prefix), or zero, if none can be found on J.
Again referring to figure 2,
``XLASLCF(LPTS)`` ⇒ γ, the last l-word on ``LPTS``.
``XTGSCHF(XCARF(LSEG), 1)`` ⇒ μ4, an l-word on μ1 (segment AB),
----------
μ1
containing the machine name of a segment equal to segment AB in
its address field.
``XBSPSHF(XCARF(LSEG), 4)`` ⇒ μ2, an l-word on μ1 containing a bit
in the sign position.
The operations described thus far are characterized by the fact that they all manipulate or process information on lists that already exist in NSS storage. In order to generate new lists, the operation of removing a cell from available storage must be introduced into the system. The latter process is the distinguishing property of the list-generating functions. Fundamental among these are the following:
XDWORDF(J).
The full 36-bit word J is stored in a cell removed from LAVST. The value of the function is the address of that cell.XLWORDF(JSP,JD,JA,JT).
JSP and JT are 3-bit quantities. JD and JA are 15-bit quantities. A cell is removed from LAVST and JSP, JD, JA, JT are installed in the signed prefix, decrement, address and tag fields of that cell, respectively. The value of the function is the address of the cell.
Arbitrary list structures may be generated by combining XDWORDF and XLWORDF according to the FORTRAN rules for the algebraic composition of functions. Thus, let us supppose that in the course of the machine's attempt to find a proof for a particular theorem, a new point is constructed with x- and y-components XCOMP and YCOMP, respectively. The point has been given a symbolic name, NUNAME, by calculation of the earliest letter of the alphabet that has not yet been used. The single statement displayed below will generate a point list for NUNAME and insert it on LPTS at the beginning of the list (fig. 3) [6]. (Note that one could as readily attach the new point anywhere on LPTS, and at the end in particular by using XLASCF(LPTS).)
LPTS = XLWORDF(3, LPTS, XLWORDF(2, XLWORDF(2, XLWORDF(0, XLWORDF(0,
0, NUNAME, 0), XCADF(XCDAF(LPTS)), 0), XDWORDF(YCOMP), 0),
XDWORDF(XCOMP),0),0)
| [6] | Because the correspondance between lists and FLPL expressions, this statement can be formulated in the time it takes to write it down, despite its complicated appearance. |
The following correspondance is seen to exist between nested list-generating FLPL expressions and an NSS list. Nesting of XLWORDF functions in the decrement variable position of XLWORDF corresponds to the linear stringing of l-words in a list. A "decrement nest" of XLWORDF functions in the address variable position of an XLWORDF function corresponds to a sublist on the list containing that instance of XLWORDF. Alternatively, the address variable may be an XDWORDF function, corresponding to the entry of a d-word, or may be a 15-bit symbol. The signed prefix and tag fields may of course, be 3-bit variables, rather than the constants illustrated above. These properties are clearly recursive in each instance of XLWORDF in an FLPL expression.
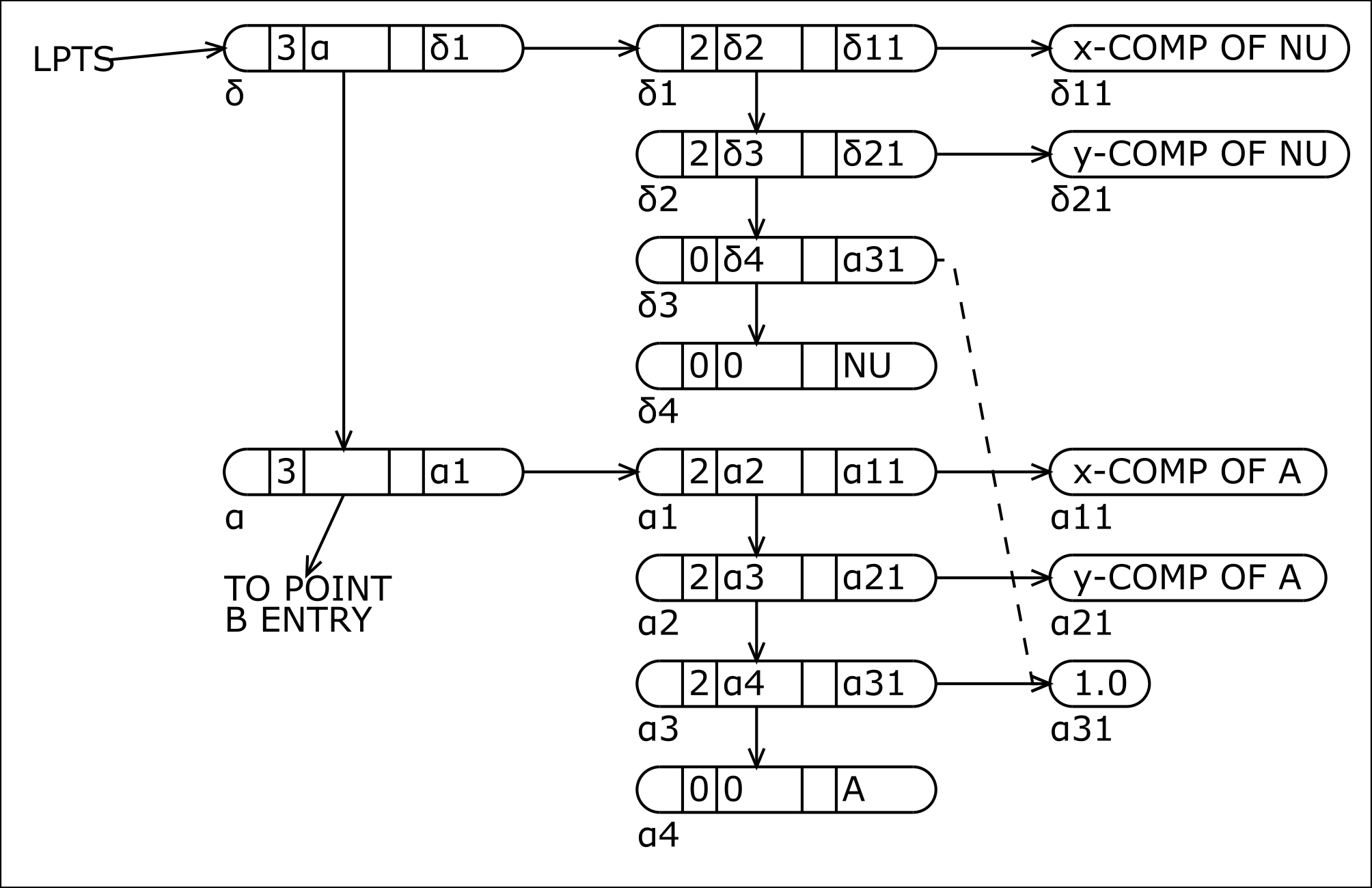
Fig. 3. Configuration of LPTS after the addition of point NUNAME (abbreviated NU above) to the list.
Here, again, it is convenient to include among the primitive FLPL functions a certain number of specialized list-generating processes even thought hey may readily be defined in terms of the primitives already mentioned. Thus, a set of "XCOPY" functions enables one to reproduce a given list in any desired configuration, the "XINSERT" series of functions enables one to introduce data at anay point in a list, and so on.
Input, output, monitoring, and "housekeeping" routines are classified as service functions. Together with the functions already described, they comprise a complete NSS list processing language. Included in this class are:
XSTARTF(J,K).
Converts the block of standard 704 core storage starting at location J and ending at K into NSS storage by placing each cell on LAVST.XTOERAF(J).
Erase the entire list J including all data and sublists belonging to J.XERASEF(J).
Erase the single l-word and associated data word (if one is present), where J contains in tis decrement the address of the word to be erased.XDUMPF(J, ± T).
NSS list output routine used extensively for debugging. J is the list to be written on output tape unit T. If T is positive, all borrowed lists are printed; if negative, only sublists that belong to J are printed.CLOCKF(O).
Reads time clock. Has as its value in floating point form the true time of day to the nearest hundredth of a minute.
Other input-output routines are available for storing data lists on tape and reading them back into NSS storage.
Finally, a particular FLPL library will generally have among its primtives a number of functions that are rather specialized to the problem at hand. Members of this class all perform complex operations that are called for with great frequency, so that it is useful to seek greater efficiency than could be attained if they were defined within FLPL. They may be easily written by first defining them within FLPL and them "streamlining" the resulting compiled SAP routines.
IV. Concluding Remarks
FLPL has been, in a sense, specifically "product-developed" for the geometry theorem-proving program, and thus far the latter is the only large-scale program written in that language. The geometry program, however, comprises three largely dissimilar subsections which span the entire range of complex information-processing opertions [2]. On one hand the syntax computer deals almost excllusively with uninterpreted symbolic expressions, while on the other hand the diagram computer is mostly concerned with a highly structured array of numerical data. The heuristic computer, which serves as an intermediary between syntax and diagram computers, must process both kinds of information, interpreting symbolic expressions as numerical equations and converting numerical data into abstract symbolic expressions. On this basis it is reasonable to claim a fair degree of universality for FLPL, providing only that the requirements of the problem indicate the desirability of an NSS organization of storage.
It is interesting to compare FLPL with IPL V, a Newell-Shaw-Simon interpretive list-processing language soon to be available for the IBM 704. In IPL V, Newel, et al, have solved the problem of list priority assignment in much the same way that the authors have, by assigning the equivalent of our type code to each l-word. Both languages are able to perform identical list-processing operations with the following exceptions. FLPL contains, in addition to the processes described in section III, all legitimate FORTRAN operations, so that the entire floating point arithmetic power of FORTRAN is at the programmer's disposal, together with the convenient input, output, indexing, and format processes vailable in FORTRAN. Too, the diagnostic services performed by FORTRAN offer great aid and comfort to the programmer. On the other hand, because IPL V completely discards the accumulator as a means of communication between IPL subroutines, substituting instead an NSS communication list, one may define routines recursively within the framework of IPL V. ALthough it is possible to do a limited amount of recursion within FLPL by purposefully saving all intermediate results and index registers in NSS lists, the authors have not yet felt the need to experiment with this mode of operation, since the traditional looping procedures have served the purpose well.
Higher list-processing routines may easily be defined within either language, although perhaps here FLPL maintains a slight edge over IPL V in the vareiety of procedures whereby such routines may be constructed and named. In the other direction, the inclusion of basic machine language instructions within the vocabulary of the language is a decied advantage of FLPL, and one that has been pressed with great frequency in the programming of the geometry theorem-proving machine.
FLPL trades a negligible increase in program storage for a significant increase in procesing speed. In many cases, the difference in computing time required to produce results will make the difference between a program that is a useful research tool and one that is merely a curiosity. For a typical problem appearing in a high-school geometry examination, our FLPL-programmed geometry machine requires a reasonable twenty minutes. The authors fell that the two hours required by the same program written in IPL V would be an excessive amount of time to allow the machine to search for a proof.
Comparison of the two languages in terms of programming convenience is largely taste-dependent. Again, the authors fell that an algebraic compounding of mnemonically-named expressions is preferable to a linear sequencing of "catalog-number" designated routines, but programmers experienced in the use of IPL seem to find little advantage in the change of program format. A new programmer, unless he has had previous training in the use of FORTRAN, is likely to require about the same amount of time to gain proficiency in either language.
One feature of IPL V is excluded from FLPL by the nature of a compiler. Sequences of IPL instructions to be intrepreted are stored in the computer as NSS lists, just as are the data. Although this property has been largely irrelevant to all programs written to date, it is conceivable that one might want to write a program in which the symbolic entities that are processed are IPL instructions themselves, and in which transfers of control take place between the meta-program and the machine-generated one. The fact that the transformation of FLPL expressions into computer activity is a two-stage, irreversible process places this kind of behavior beyond the range of our language, even though it is quite feasible to manipulate FLPL expressions within FLPL.
REFERENCES
- Gelernter, H. and Rochester, N., Intelligent behavior in problem-solving machines, IBM J. Res. Dev. 2 (1958), 336-345.
- Gelernter, H., Realization of a geometry theorem-proving machine, Proc. Int. Conf. on Information Processinng, Unesco, Paris (1959), to be published.
- Newell, A., Shaw, J. C., and Simon, H. A., Empirical explorations of the logic theory machine, Proc. of the western Joint Computer Conference, (1957), pp. 218-230.
- Minsky, M. L., Some methods of artificial intelligence and heuristic programming, Proc. Symposium on the Mechanization of Thought Processes, Teddington (1958).
- Newell,l A. and Shaw, J. C., Programming the logic theory machine, Proc. of the Western Joint Computer Conference, (1957), pp. 230-240.
- Wang, H., Toward mechanical mathematics, IBM J. Res. Dev. 4, No. 1 (1960).